Pizza Fractions Explained: Your Guide To Understanding Orders
Can the simple act of ordering a pizza reveal a deeper understanding of mathematical principles? The answer lies within the seemingly straightforward requests, where fractions, division, and proportional reasoning come to life.
The quest for the perfect pizza often leads to a playful exploration of mathematical concepts, masked by the delicious anticipation of a meal. Consider the opening conundrum: "We did not find results for: One fourth of two pizzas." This seemingly simple phrase immediately plunges us into the realm of fractions. "One fourth" (1/4) represents a portion of a whole, in this case, a pizza. The question then becomes: what does it mean to take one-fourth of two pizzas? It means dividing the total amount of pizza into four equal parts and considering one of those parts. This showcases an intuitive understanding of division and its relationship to fractions.
The culinary canvas further expands with requests such as "One pizza with sauce cheese and basil, and one pizza with sauce and cheese on both halves, basil on half, and anchovies on the other half." While seemingly unrelated to fractions at first glance, this order presents opportunities to contemplate portions. The demand for "basil on half" introduces the concept of dividing a pizza into two equal parts, a fraction of 1/2. Simultaneously, the presence of anchovies on one side introduces the possibility of creating even more elaborate variations through fractions.
The interaction then pivots to the user's dilemma "My math midterm is today, and i need to learn about fractions!" This reveals the underlying motivation. They are not merely ordering pizza; they are learning about fractions. This is confirmed in several subsequent instances: "\u201cone third of a dozen\u201d = 4 \u201cdivided by two\u201d = 2 2 pizzas" illustrates the connection between division and fractions in real-life problems. Similarly, the user seeks to understand the practical application of these mathematical concepts, with pizza orders serving as an accessible context for learning. The phrase, "\u201ci need one half of four pepperoni pizzas.\u201d recipe:" further underscores this, tying a recipe directly to the concept of fractions.
The user then explores further complexities, with expressions like "Ok so, i can't remember the exact details but i remember something about wanting 3\/4 of two pizzas with anchovies and 1\/4 i think of both pizzas with basil." This is a great exercise in understanding fractions. "3/4 of two pizzas" can be interpreted as finding the amount of anchovy pizza required when taking three out of four portions of pizza, with the total being two pizzas. The "1/4 i think of both pizzas with basil" represents taking one quarter of the amount and having basil on it. The confusion surrounding the order highlights the nuanced nature of these fractional concepts. The user's uncertainty reinforces the value of making the mental process of interpreting and executing these fractional concepts.
Another order reveals: "As for the rest of it, half of the order should have sausage, so one pizza worth of sausage. Half of that sausage is on wheat. 1 wheat crust pizza with 1/2 sausage and 1 plain crust with 1/2 sausage." This order demonstrates how a simple fraction can be applied when ordering pizza. "Half of the order should have sausage," means one out of two portions of the order needs to have sausage. Further, half of that sausage is on wheat, further fractioning the ingredients. It also showcases the capacity of fractions to be applied to real life situations.
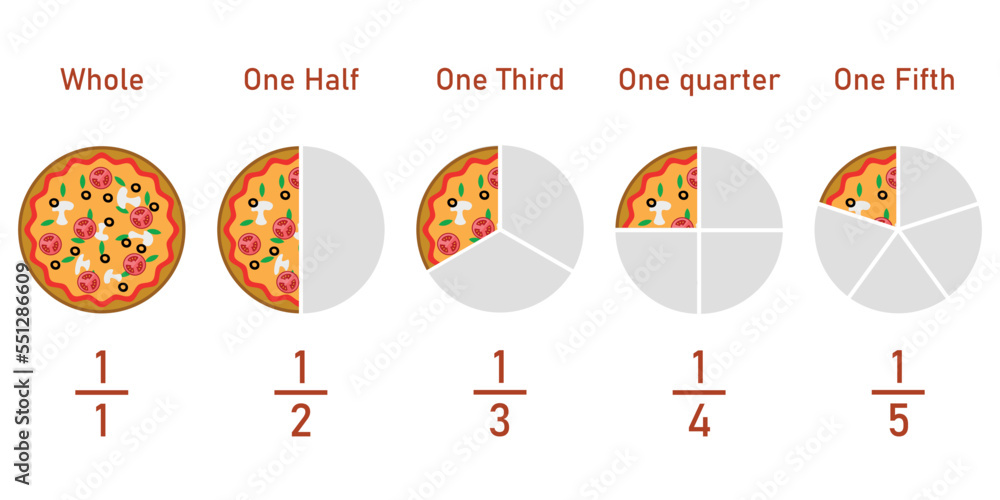
The discussion then delves into the core tenets of fractions. Several exchanges directly address core concepts. For instance, statements like "Both terminologies refer to 25% of the total pizza," clarify the relationship between fractions and percentages, where 25% is equivalent to 1/4. Further, "Here, the fraction is written as: Here, the numerator 1 says that one slice of pizza is left. And the denominator 4 says the pizza is cut into 4 equal slices," providing a clear explanation of numerator and denominator and how they represent different aspects of a fraction. Additional insights, such as "What are quarters in fraction? The quarter in fraction is one out of 4 equal parts. It is written as 1 4" offer clear answers to key questions in the world of fractions.
The application of fractions within the context of pizza orders continues to appear: "He wants two pizzas, one wheat and one regular dough. Sausage on half (3 slices) of each." It demonstrates a combination of different ideas of fractions, showing how fractions and ordering of pizza are related, from the number of pizzas to the toppings. This illustrates how to divide each pizza into two halves (1/2), with three slices on the pizzas.
The exchanges then proceed with problem-solving prompts, challenging users to analyze various fractional scenarios. For instance, "A 3/8 pizzas b 1/2 pizzas c 5/8 pizzas d 3/4 pizzas \u201cone half of 4\u201d means 4 divided by 2, which is 2 pepperoni pizzas" This is a direct calculation where the user must apply their knowledge of division and fractions to solve. "If you get stuck on these math orders, you can find them on the list of orders page :) 0," shows how users can use different resources to learn more about fractions. Moreover, other examples like "Two pizzas, one half basil half anchovy, the other just anchovy," introduce the concepts of fractions further, and the value of how different ingredients are allocated.
As an advanced exercise, the user then engages with more complex examples. "One pizza split into half would be 1/2, so with two pizzas each split into half a half would be 1/4," which highlights how the concept of fractions can be applied. The complexity of the concept grows with the next instance: "There is 6/9 of a pizza left over, and three people share it equally." It showcases the application of fractions and division in a scenario. And, "When 3/4 is divided equally between two people, one fourth piece must be split into two," demonstrating how to divide a fraction by a whole number. Similarly, "What is one fourth of a pizza? See answer (1) best answer. A) 3/8 pizzas b) 1/2 pizzas c) 5/8 pizzas d) 3/4 pizzas," further emphasizes problem-solving through fractions.
The discussion's purpose becomes to delve into the fundamentals of fraction, with statements such as, "For example, when a pizza is cut into four pieces, each piece is a fraction of the pizza. Fractions consist of two numbers: The numerator, which is the number above the line, and the denominator, which is the number below the line. If you think of a pizza again, and we take one slice out of the four, our fraction is 1/4. 4 1 = slices # of one \u2212 slice size of fourth in the fraction above, the numerator is 1 and the denominator is 4." These concepts can then be directly applied to pizza ordering to illustrate the real-world relevance of these topics. Examples include, "She cuts it into 3 equal pieces," this showcases fractions when dividing. "What fraction of a yard is each piece of fabric?, four friends share 3 apples equally. She pours the same amount into each of 3 glasses. What fraction of a quart is in each," These examples highlight fraction in real life application.
Finally, the conversation concludes with problems, such as, "One day the pizza shop makes 6 pizzas. How much more money will they make if they slice all the pizzas into eighths than if they slice the pizzas into fourths?" Such questions challenge the user to apply their understanding to calculate cost differences. Through these examples, the interaction transforms into a practical lesson on fractions. The core of the interaction is the process of taking fractional parts from the total. Furthermore, ordering pizza provides an understandable context to analyze the fractional concepts, making it easier to learn and comprehend these ideas.
| Concept | Explanation | Pizza Example |
|---|---|---|
| Fraction Basics | A fraction represents a part of a whole. It is written as a numerator (the top number, representing the part) over a denominator (the bottom number, representing the whole). | 1/4 of a pizza means the pizza is divided into 4 equal slices, and you have 1 of those slices. |
| Numerator | The top number in a fraction, it indicates how many parts of the whole you have. | In 3/4 of a pizza, the numerator (3) indicates you have 3 slices. |
| Denominator | The bottom number in a fraction, it indicates how many equal parts the whole is divided into. | In 1/4 of a pizza, the denominator (4) indicates the pizza is cut into 4 equal slices. |
| Halves (1/2) | Dividing something into two equal parts. | One half of a pizza means the pizza is cut in two equal slices. |
| Quarters (1/4) | Dividing something into four equal parts. | One quarter of a pizza means the pizza is cut into four equal slices, and you take one of the slices. |
| Thirds (1/3) | Dividing something into three equal parts. | One third of a pizza means the pizza is cut into 3 equal slices, and you have 1 of those slices. |
| Eighths (1/8) | Dividing something into eight equal parts. | If a pizza is sliced into eighths, each slice represents 1/8 of the pizza. |
| Fraction Operations (Addition, Subtraction) | Fractions can be added, subtracted (with common denominators). | If you have 1/4 of one pizza and 1/4 of another, you have 2/4 (or 1/2) of a pizza. |
| Fraction Operations (Multiplication) | Multiplying a fraction by a whole number or another fraction | "Half of 4 pizzas" (1/2 * 4 = 2 pizzas). |
| Division with Fractions | Dividing something into parts or sharing equally. | If 3/4 of a pizza is shared by 2 people, each person gets 3/8 of the pizza. |
| Fractions and Percentages | Relating fractions to percentages (e.g., 1/4 = 25%). | "Both terminologies refer to 25% of the total pizza." |
| Problem Solving | Apply fractional concepts to real-world scenarios. | Calculating how much more pizza is available if sliced into eighths vs fourths. |
The use of pizza provides an approachable, everyday context for exploring complex mathematical concepts. It turns the learning process into a pleasant experience. This offers a real-world context to apply the concepts, which are more relatable. Moreover, the questions and discussions also help you to improve your understanding of fraction concepts. This type of exercise promotes critical thinking and problem-solving skills.